Systems biology aims at getting a higher-level understanding of living matter,
building on the available data at the molecular level. In this
field, theories and methods from computer science have
proven very useful, mainly for system modeling and simulation. Here we argue
that languages based on
timed concurrent constraint programming (timed ccp) --a well-established model for concurrency
based on the idea of partial information-- have a place
in systems biology. We summarize some works in which our group has
tried to assess the possibilities/limitations of one such formalisms in this domain.
Our base language is
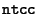
, a non-deterministic, timed ccp process calculus that provides a
unified framework for modeling, simulating and
verifying several kinds of biological systems. We discuss how the interplay
of the operational and logic perspectives that
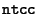
integrates greatly favors
biological systems analysis.

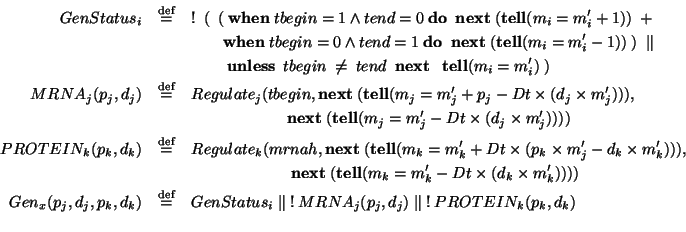
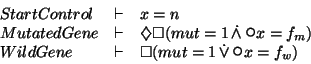
![\begin{displaymath}
\infer [\mathsf{LPAR}]
{StartControl \parallel MutatedGene...
... \vdash \sometime \always ( mut=1 \tand \nextt x=f_m ) }{}
}
\end{displaymath}](img63.gif)
![\begin{displaymath}
\infer [\mathsf{LPAR}]
{WildGene \parallel SC \parallel MG...
...(~ \sometime \always ( mut=1 \tand \nextt x=f_m ) ~) ) }{}
}
\end{displaymath}](img70.gif)
![\begin{displaymath}
\infer [\mathsf{LCONS}]
{ControlRegion \vdash \sometime \a...
...sometime \always ~( mut=1 \tand \nextt x=f_m ) ~) } {}
}}}}}
\end{displaymath}](img73.gif)