Will it rain today given that we see clouds? You likely know how to count apples or coins, but how do you count over the possible worlds where it is cloudy and raining? That is exactly the task of model counting, which forms a simple but powerful approach to reason over uncertain outcomes and compute probabilities such as whether it will rain.

In this post we provide the intuition to understand the fascinating world of model counting: what is it, why is it so important (state-of-the-art probabilistic reasoning algorithms!), and what is the relation with knowledge compilation.

What is model counting?

Consider the following example: there are two variables $A$ and $B$, that are both Boolean (meaning, they can be either true or false). As a consequence, there are four possible truth assignments, listed below.

1. A is true, B is true
2. A is true, B is false
3. A is false, B is true.
4. A is false, B is false.

How many of these assignments satisfy the constraint “A is true or B is true”? This is a model counting question, and the answer is three.

More formally, model counting is a computational problem where we are given a set of constraints and need to determine the number of assignments satisfying those constraints. Typically, the constraints are defined using logic formulas. For example, $A \lor (\neg A \land B)$ means that “A is true, or A is false and B is true”. In logic, when an assignment satisfies the constraints we call it a model, hence the name model counting.

Example Let us consider a larger example with the following constraints:

• It rains if and only if it is cloudy and humid.
• You get wet if and only if it rains or the sprinklers are on.

This can be encoded into a logic formula $ (rain \iff cloudy \land humid) \land (wet \iff rain \lor sprinkler)$

The model count of this example is $2^3$. We list the models in the image below; we will call these ‘possible worlds’.

Suppose that we wish to only count those models where $wet$ (the last column) is true, that is, we extend the logic formula with $\land wet$. The total model count is then 5.

Note that model counting is a direct extension of the well known satisfiability problem, which is merely concerned with determining whether there exists at least one satisfying assignment, as opposed to determining the exact count (cf. the SAT Game).

Why do we care? Probabilistic reasoning!

Suppose furthermore that each of the possible worlds (models) in the previous example have a probability. By counting only those where $wet$ is true, we are then essentially computing the probability that $wet$ is true. That is, model counting can be used to perform probabilistic reasoning!

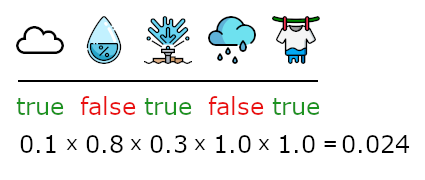
While the above example uses probabilities, a weighted model counting problem supports any numerical weight. Usually, rather than directly defining a weight for each model, we instead use a weight function $w$ that defines a weight for when a variable is true, and for when it is false. The weight of a model $m$ is then obtained by multiplying the relevant weights: $\prod_{l\in m} w(l)$.

Example Consider the previous example. We could associate a probability with $cloudy$, $humid$ and $sprinkler$. For instance:

• $w(cloudy) = 0.1$, $w(humid) = 0.2$, $w(sprinkler) = 0.3$,
• $w(\neg cloudy) = 0.9$, $w(\neg humid) = 0.8$, $w(\neg sprinkler) = 0.7$

Since the truth values of $wet$ and $rain$ are completely defined by the other three variables, we set their weights to $1.0$:

• $w(rain) = 1.0$, $w(wet) = 1.0$,
• $w(\neg rain) = 1.0$, $w(\neg rain) = 1.0$

In this way, the total weight of a model is exactly the probability of the possible world that it represents. This is illustrated in the figure below, where the probability of the possible world is $0.024$. Since $humid$ is false in the possible world, the equation uses $w(\neg humid) = 0.8$.

Weighted model counting More formally, the weighted model count (WMC) of logic formula $T$ with weight function $w$ is defined as the equation below, where $M(T)$ denotes the set of models of $T$ (that is, the possible worlds).

$WMC(T) = \sum_{m \in M(T)} \prod_{l \in m} w(l)$

In this equation, we compute the weight for each model $m$ (the product operation), and sum the results to obtain the weighted model count.

Example Continuing the previous larger example with the aforementioned weights, the total weighted model count is $1.0$ (try it yourself!). If we additionally add $\land wet$, that is, consider only those models where $wet$ is true, then the weighted model count becomes $0.314$, exactly the probability that $wet$ is true (try it yourself!).

We can also compute conditional probabilities. For example, imagine that we observe the sprinkler to be off and want to know the probability that we get $wet$. Using probability theory, this is computable via two weighted model counts:

$Prob(wet | \neg sprinkler) = Prob(wet \land \neg sprinkler) / Prob(\neg sprinkler)$ $Prob(wet | \neg sprinkler) = WMC(T \land \neg sprinkler \land wet) / WMC(T \land \neg sprinkler)$

Efficient counting via knowledge compilation

Variables are true or false, so in the worst case there are $2^N$ models with $N$ the number of variables. Since this is exponential, naively counting models one by one quickly becomes infeasible as the number of variables increases. Fortunately we can often do much better in practice!

Example Consider computing the weighted model count of the previous example while including $\land wet$. Naively iterating over the 5 models and computing the weighted model count involves 20 multiplications and 4 additions. In the image below we show how to perform the same count but with fewer operations (8 multiplications and 4 additions) by exploiting distributivity, commutativity and associativity.

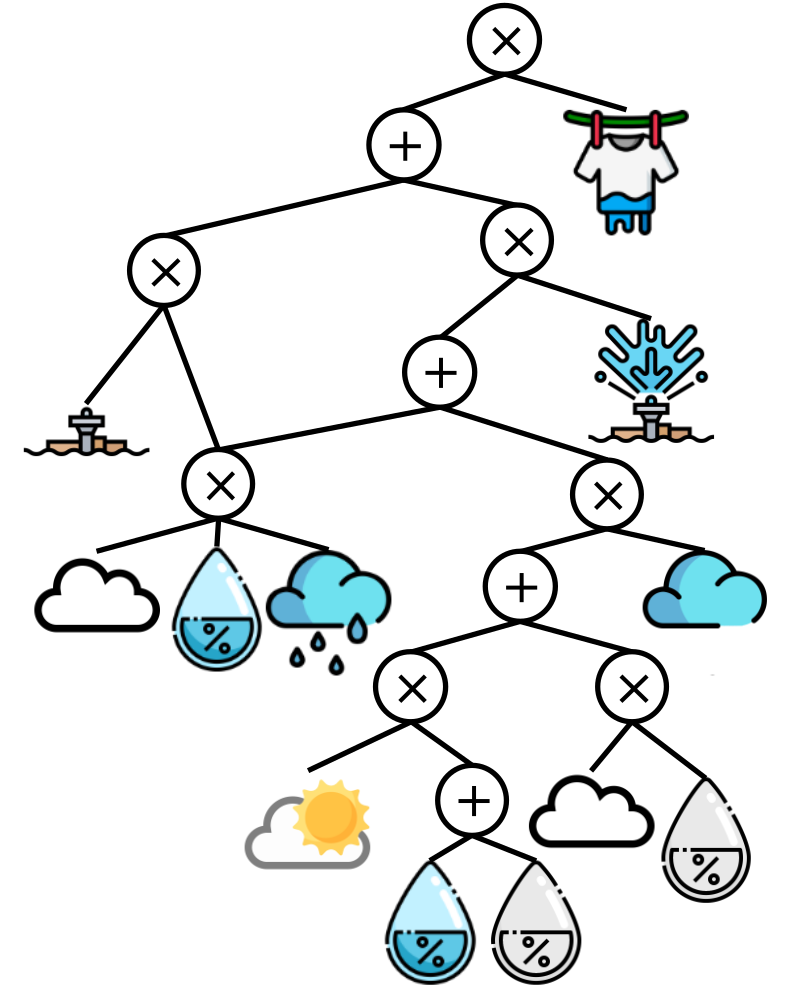
In the domain of knowledge compilation, researchers have produced algorithms that can automatically create such compact representations from a given logical formula, in a way that allows us to easily compute the weighted model count.

Conclusion

In conclusion: we first explained what model counting is, namely, counting in a weighted fashion the number of assignments satisfying a given logical formula. We then hinted to the importance of this computational task by providing an intuition on how it models probabilistic inference problems and thereby contributes to state-of-the-art probabilistic reasoning algorithms. Finally, we mentioned knowledge compilation, a research domain that helps to solve counting tasks more efficiently by restructuring the logical formula.

If you wish to learn more about how to use model counting for state-of-the-art probabilistic reasoning, we kindly refer to

• On probabilistic inference by weighted model counting. M. Chavira, A. Darwiche. Artificial Intelligence, 2008.

If you instead wish to learn more about how to automatically count models, check out our conference paper that improves the model counting process by exploiting structural symmetries!

• Symmetric Component Caching for Model Counting on Combinatorial Instances. T. van Bremen, V. Derkinderen, S. Sharma, S. Roy, and K. S. Meel. AAAI, 2021.

We acknowledge the authors of the used icons:

• Humidity icons created by justicon - Flaticon
• Rain icons created by tulpahn - Flaticon
• Wet icons created by Smashicons - Flaticon
• Sprinkler icons created by Eucalyp - Flaticon
• Cloud icons created by Freepik - Flaticon
• Summer icons created by Freepik - Flaticon