Hierarchical Arc Consistency for Disjoint Real Intervals in Constraint LP

Appeared in Volume 6/1, February 1993

Keywords: constraints.

Extended Abstract¹
Greg Sidebottom and William S. Havens

1. Introduction

There have been many proposals for adding sound implementations of numeric processing to Prolog. Many constraint LP (CLP) languages use symbolic constraint solving techniques for linear constraints. CHIP and BNR Prolog use consistency and case analysis algorithms (Mackworth, 1977) for solving constraints. This paper describes an approach to real numeric constraint processing which has been implemented in Echidna, a new CLP language. Like CHIP and BNR Prolog, Echidna uses consistency algorithms which can actively process a wide variety of numeric constraints. The key difference is that Echidna implements domains which are disconnected sets using a hierarchical data structure and exploits this structure using a hierarchical arc consistency algorithm (Mackworth, Mulder and Havens, 1985) which is specialized for numeric constraints. The hierarchial datastructure makes it possible to represent disjunctive information directly.

Echidna can handle such general systems of constraints because it uses partial consistency algorithms. Normally, consistency algorithms compute solutions to sets of constraints. Partial consistency algorithms approximate the set of solutions with a super-set. Good partial consistency algorithms compute a super-set which is only slightly bigger than the actual set of solutions for a substantially reduced cost. Echidna's algorithms are easily parameterized to compute arbitrarily close to the actual set of solutions.

2. Numeric Constraints in the Echidna Language

This section describes the particular extensions to Edinburgh syntax Prolog which are relevant to numeric constraint processing and takes some liberties with syntax. Echidna provides domain constraints, equalities, inequalities, and disjunctions of inequalities on real numeric expressions. A domain constraint is a unary constraint of the form 'X in Set' where X is a real valued variable and Set denotes the domain of X. The Set in a domain constraint is specified by a finite union of real intervals. Equalities and inequalities constrain real numeric expressions. Expressions are built up from variables and real constant symbols using numeric function symbols². Echidna also supports disjunctive inequalities constraints of the form 'C1 or C2' where C1 and C2 are inequalities. For instance, Figure 1 gives an Echidna program for scheduling tasks using some of the relations on temporal intervals. A task is represented by a term task(S, D) where S is the start time of the task and D is the duration of the task. The predicate, in(Task, SuperTask), is true if the interval for SuperTask contains the interval for Task. NoOverlap(Task, Tasks) is true if Task overlaps with none of the tasks in the list Tasks. It uses a disjunctive inequality constraint to make sure Task is either before or after each of the tasks in Tasks. Schedule(Tasks, SuperTask) is true if all the tasks in the list Tasks are in SuperTask but no pair in Tasks overlap.

in(task(S1, D1), task(S2, D2)) :-
	S1 >= S2,
	S1+D1 <= S2+D2.

noOverlap(_, []).
noOverlap(task(S1, D1), [task(S2,D2)|Tasks]):-
	S1+D1<=S2 or S1>=S2+D2,
	noOverlap(task(S1, D1),Tasks). 

schedule([], _).
schedule([Task | Tasks], SuperTask) :-
	in(Task, SuperTask),
	noOverlap(Task, Tasks),
	schedule(Tasks, SuperTask).

Figure 1. An Echidna Program for scheduling tasks

3. Overview of Echidna's Implementation

Echidna programs are executed by an SLD-resolution theorem prover which incrementally constructs and maintains a constraint satisfaction problem (CSP). A CSP consists of a set of variables, each associated with a domain of possible values; and a set of constraint relations on subsets of the variables which specify values to which those variables can simultaneously be assigned. The notation D(X) is used to denote the domain of the variable X. When a constraint is selected by the theorem prover, it is added to the CSP. Echidna manipulates the CSP using two kinds of algorithms (Mackworth, 1977):

arc consistency is used to remove inconsistent values from the domains of variables participating in numeric constraints, and
case analysis is used to consider, alternatively, different halves of real variable domains.

If the arc consistency algorithm ever removes all values from a variable domain, the theorem prover backtracks using dependency backtracking (Havens, 1991). Backtracking through a constraint consists of removing it from the CSP.

The case analysis algorithms implement a divide and conquer search for solutions to the CSP. The arc consistency algorithms are interleaved with the case analysis algorithms to help reduce the search space. The case analysis algorithm is accessed by the built in predicate split(Vars). Split(Vars) repeatedly cycles through the list Vars of variables in a round robin fashion removing approximately half the values in each variable's domain. Upon backtracking, split will restore half of a domain and remove the other half. Currently, the number of times each variable in a list can be split is determined by a call to the built in predicate precision(Vars, Prec).

4. Numeric Hierarchical Arc Consistency

This section describes HACR, the hierarchical arc consistency algorithm Echidna uses for real numeric constraints. We use the notation v(C) to denote the set of variables in the constraint C. We assume the CSP is formulated as a directed hypergraph where variables are associated with nodes and each constraint C is a set of hyperarcs of the form (T, C) for each T in v(C). T is called the target and the rest of the variables in v(C) are called sources. Let C be a constraint with v(C) = {X(1), X(2), I, X(k)}. The notation pi(X(i),C) means the result of projecting the constraint C onto the variable Xi. More formally,

pi(X(i),C) =
    {a(i) in D(X(i)) | there exists (a(1),...,a(i-1),a(i+1),...,a(k)) in
    D(X(1))x...xD(X(i-1))xD(X(i+1))x...xD(X(k)
    such that C(a(1),...,a(k))}.

Full arc consistency algorithms terminate with D(T) = pi(T,C) for every hyperarc (T, C) which formulates the CSP. Partial arc consistency algorithms set D(T) to some efficiently computable superset of pi(T,C). HACR is a partial arc consistency algorithm based on the full hierarchical arc consistency algorithm HAC (Mackworth, Mulder and Havens, 1985). Both are similar to AC-3 (Mackworth, 1977), but they use different arc revision algorithms which operate on hierachically structured domains. HACR represents a domain such as [1,1.875] U [3.75, 4] using the structure shown in figure 2 (in the hardcopy version of this abstract). The root's interval contains the domain and the intervals for the two children of an node are roughly the lower and upper halves of the their parent's domain. The relationship between a parent and its children's is:

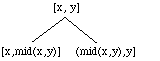
where x < mid(x,y) < y. The types of boundary (open or closed) associated with x and y in the children are inherited from parent and one of the boundaries associated with mid(x,y) is open while the other is closed. A node is marked 'c', '?', or 'x' if, respectively, all, some (but not all), or none of the numbers in its interval are in the domain. The trees are conceptually infinite but only a finite part needs to be examined by HACR. The intervals can be computed using the path from the root, so no intervals are stored at each node.

For a hyperarc (T, C), HACR deletes values outside pi(T,C) by manipulating the marks in the tree representing D(T). A set of intervals whose union is pi(T,C) is generated one at a time and a new value for D(T) is accumulated by adding an approximation of each interval to it. HACR would be a full arc consistency algorithm if the marks could each D(T) could be set exactly to pi(T,C). However, with any a priori splitting strategy, it is possible that an an unbounded amount of refinement will be required. Since real domain trees are infinite, a full arc consistency algorithm using these trees may require infinite space and may not terminate. Instead, HACR associates a non-negative integer precision P(X) with each variable X. P(X) is the maximum distance from the root to any node in the tree for D(X) which will be accessed by HACR. Thus, at any particular point, HACR can only access a finite part of each domain tree. The Echidna built in predicate precision(Vars, P) sets the precision of each variable in the list Vars to P. When HACR determines that a node should be refined, that is its mark should be set to '?' and its children analyzed, if the node is at the precision limit then its mark is left 'c'. For this reason, ReviseHACR is a partial arc revision algorithm, but it can be made arbitrarily close to a full arc revision algorithm by increasing the precision of variables. If the predicate precision is used to increase the precision of a variable X, then HACR is reinvoked because it may be possible to refine D(X) and some other domains.

A set of intervals whose union is pi(T,C) is generated differently for each class of constraint. All complex constraints are broken down into an equivalent set of constraints using at most one numeric function each using intermediate variables.

For an equality, pi(T,C) is computed by solving C for T. Then, the projection is generated by iterating through all the combinations of intervals marked 'c' in the source domains. This is done by traversing the fringe of domain trees and combining adjacent intervals marked 'c'. The numeric function used in the constraint is then applied to each pair of intervals using formulas such as:

[x1, x2] + [y1, y2] = [x1+y1, x2+y2],
[x1, x2] - [y1, y2] = [x1-y2, x2-y1],
[x1, x2]*[y1, y2] =
	[min{x1*y1,x1*y2,x2*y1,x2*y2},
         max{x1*y1,x1*y2,x2*y1,x2*y2}], and
[x1, x2] / [y1, y2] = [x1, x2]*[1/y2, 1/y1].

Limit values are used where functions are discontinuous (eg. division by 0). It is easy to verify that the projection of an inequality of the form 'T <= S' is:

pi(T,C) = [min D(T), max D(S)]

and other inequality cases are similar.

For a disjunctive inequality of the form C1 or C2,

pi(T,C1 or C2) =
	pi(T,C1) U pi(T,C2)  if T in v(C1) and T in v(C2)
	< D(T)   if T in v(C1) and T notin v(C2) and C2 is satisfiable
	pi(T,C1) if T in v(C1) and T notin v(C2) and C2 is unsatisfiable

5. Examples

This section contains example runs of Echidna version 1.0 on a Sun Sparcstation. Echidna can numerically solve polynomials with varying precision using the built in predicate precision. Consider the following query, where, as described in section 3, precision([X], 8) sets the precision P(X) of the variable X to 8 bits and the call split([X]) invokes a case analysis algorithm to search for solutions for X.

?-   X in [-1000, 1000), precision([X], 8), 
      (X - 1)*(X - 2) = 0, split([X]).

Since Echidna's numeric constraint solving system is incomplete, Echidna outputs approximate answers but guarantees that all solutions to the query are present in some answer. For this query, Echidna computes the following three answers:

X in [0, 7.8125)       ; % both solutions here
X in [7.8125, 15.625) ;
X in [15.625, 23.4375) ;
no.

More precise approximations of the solution can be obtained by computing CSPs with smaller domains. Echidna can be used to do this by setting P(X) higher. For instance, if P(X) is set to 32, then the following CSPs are computed.

X in [0.9999997, 1.0000002) ;
X in [1.9999998, 2.0000003) ;
no.

For an example with disjunctive inequalities, consider the program given in figure 1 with the query:

?-  precision([S1, S2], 3), S1 N [0, 4], S2 N [0, 4],
      schedule([task(S1, 2), task(S2, 1.5)], task(0, 4)).

Echidna answers:

S1 in [0, 0.5] U [1.5, 2], 
S2 in [0, 0.5] U [2, 2.5]

All other real numeric CLP systems can only implement disjunctive constraints using explicit disjunction in the logic program.

References

Havens, W. S. 1991. Dataflow Dependency Backtracking in a New CLP Language. In Proc. AAAI Spring Symposium on Constraint-Based Reasoning. Stanford. 110-127.

Mackworth, A. K. 1977. Consistency in Networks of Relations. Artificial Intelligence. 8. 99-118.

Mackworth, A. K., Mulder, J. A. and Havens, W. S. 1985. Hierarchical arc consistency: exploiting structured domains in constraint satisfaction problems. Computational Intelligence. 1. 118-126.

Footnotes

1) The full version of this paper appears under the same title in Computational Intelligence 8(4), Blackwell Publishers, 1992. It can also be obtained by anonymous FTP. Send mail to expert@cs.sfu.ca for more information.

2) Echidna currently supports the arithmetic functions, some trigonometric functions, exponentiation, logarithm, and root extraction.

Greg Sidebottom and William S. Havens
Expert Systems Laboratory, Centre for Systems Science
Simon Fraser Univ., Burnaby BC V5A 1S6, Canada
Email: gregory@cs.sfu.ca,
       havens@cs.sfu.ca